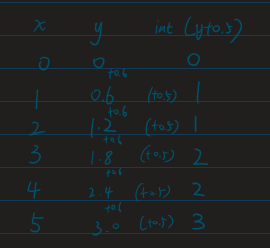直线段扫描转换算法

本文内容总结自孙家广《计算机图形学》

直线段绘制算法的发展基本是从数值微分法

到中点画线法

再到Bresenham画线算法

目前流行的渲染器使用的都是Bresenham画线算法，前两个也可以了解一下

数值微分直线算法

众所周知我们生活的现实世界的一切都是离散的（我胡说的），DDA直线算法就是用离散像素点去逼近直线段的一种算法。

我们先来看一下直线的函数表达，最常用的斜截式（顺便练练Markdown的数学公式= =）

$y=kx+b$

$k=\frac{\Delta y}{\Delta x}$

显示屏幕无论分辨率有多少总之还是一个一个点，在画线段的时候，已知两个端点，就是要把中间的点画出来，我们假设起点$(x1,y1)$，终点$(x2,y2)$，画线段时我们从x1开始，再怎么样x轴的增量也得是整数，1的整数倍，那么很自然的可以得出以下结论：

$y_i=kx_i+b$

$y_{i+1}=kx_{i+1}+b$

由于步长一定是1的倍数

$\begin{aligned} y_{i+1}&=k(x_i+1)+b\\ &=kx_i+k+b\\ &=kx_i+b+k\\ &=y_i+k\\ y_{i+1}&=y_i+k \end{aligned}$

可以发现$y$的步长增量是$k$

举个例子：

我们要画出$P_0(0,0)$到$P_1(5,3)$的直线段。

用PS随便画了一下，长这个样子：

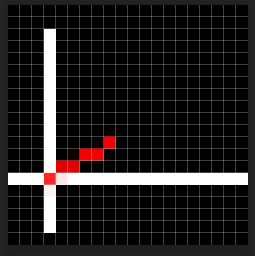
推算过程如下：

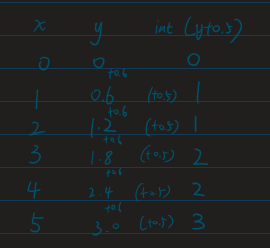
加0.5是为了向下取整的时候减少误差，比如$P(1.7,0.8)$这个点更接近的整数点应该是$(2,1)$，直接向下取整会变成$(1,0)$

那为啥不四舍五入呢

四舍五入也是加0.5再向下取整

DDA算法有比较明显的缺点，斜率大于1的线段取点会不正常：

$y=1.5x+1$

我们画一个$P(0,0)$到$P(5,8.5)$

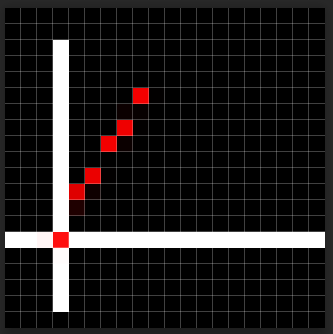
已经很难说这是个线了……取点太稀疏，中间直接断掉了

中点画线算法

这个算法在数值微分算法上改进，数值微分法步进增量一般情况下都是小数，中点画线可以改进为整数。

我们知道直线的一般式方程是这样的：

$Ax+By+C=0$

$A=-(\Delta y)$

$B=\Delta x$

$C=-B(\Delta x)$

对于直线$F(x,y)$，点有三种情况

$\begin{aligned} F(x,y)&=0\quad点在直线上\\ F(x,y)&>0\quad点在直线上方\\ F(x,y)&<0\quad点在直线下方\\ \end{aligned}$

每次在最大位移方向上走一步，另一个方向上走不走取决于中点误差

假定$0\leqslant\vert k \vert \leqslant 1$，每次在$x$方向上加1，$y$方向上只有两种情况，加1或者不加1，也就是说$P(x_i,y_i)$的下一个点有可能是$P_u(x_{i+1},y_{i+1})$或者是$P_d(x_{i+1},y_{i})$

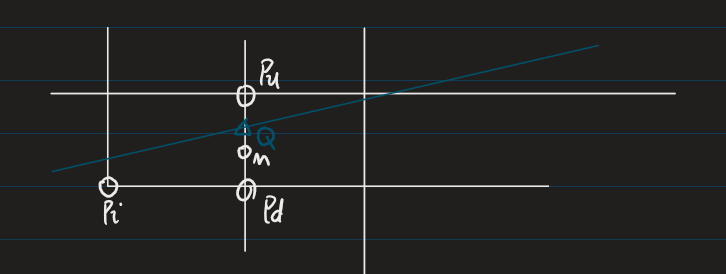
如图所示，Q是直线的理想点，M是$P_u$和$P_d$的中点$M(x_{i+1},y_{i+0.5})$

如果$Q_y$大于$M_y$说明$P_u$距离理想直线更近，否则是$P_d$更理想

那么问题就变成了怎么判断Q与M的关系

假设我们有点$P(x_0,y_0)$,那么我么下一个点$P_1$虽然不确认y值，但是下一个理想的中点$M_1(x_1+1,y_1+0.5)$是确定的，那么我们就有步进增量：

$\begin{aligned} d_{0}&=F(x_{i}+1,y_{i}+0.5) \\&= A(x_{i}+1)+B(y_{i}+0.5)+C\\&= A+0.5B \end{aligned}$

$\begin{aligned} d_{1} &= F(x_{i}+2,y_{i}+1.5)\\ &=A(x_{i}+2)+B(y_{i}+1.5)+C \\ &= A(x_{i}+1)+B(y_{i}+0.5)+C+A+B\\ &=d_{0}+A+B \end{aligned}$

实际上起点是$(0,0)$，所以有：

$\begin{aligned} d_{i}&=F(x_{i}+1,y_{i}+0.5)\\ &= A(x_{i}+1)+B(y_{i}+0.5)+C\\ &= A+0.5B \end{aligned}$

$d_0 = A+0.5B$

若$d<0$则取点$P_u$

若$d>0$则取点$P_d$

等于0随便取一个

然后就能得到关于d的步进：

$d_{new}=\left\{ \begin{aligned} d_{old}+A+B \quad ,d<0\\ d_{old}+A \quad ,d\geqslant0 \end{aligned} \right.$

当然，为了提高效率，避免浮点数加法，一般把d扩大一倍，就得到$2d_0=2A+B$

这样就是，每到下一步，先计算$d_{new}$，然后就可以判断选$y_{i}$还是$y_{i+1}$

接下来画一个中点画线法的直线：

从$(0,0)$到$(5,2)$

x	y	d
0	0	1(初始值)
1	0	-3
2	1	3
3	1	-1
4	2	5
5	2	1

Bresenham画线算法

这个算法描述起来很简单。

我们计算机画点都得是整数，第一个点直接四舍五入是一定可以确认的，那么下一个点的话，用$x$增量的话下一个必定是$x+1$，我们需要确定$y$

Bresenham画线算法计算y的误差，就是斜率k，第一个点画完后画第二个点，y的增量是k，x每增加1，误差增加k，假设误差为d，那么递增直线的误差$d = d+k$，当$d \geqslant 0$的时候就需要减去1，始终保证d在0和1之间，这样在d小于0.5的时候，y不变，否则y增加1

思路就是这个思路，当然书上对该算法进行硬件实现的时候用整数改进了除法

既然是判断d和0.5的关系，那么就是判断d减去0.5之后与0的关系，但这样开始要计算k

我们用e来表示d减去0.5

比较e和0的关系其实就只是关注e的正负号而已

代码实现的时候$e = - 0.5$（初始值），递增k，大于等于0的时候减1

首先乘2，浮点数没了，还要想一下怎么把k弄掉，k还是需要一个浮点数除法

$\begin{aligned} e &= e+k\\ 2e &= 2e + 2\frac{\Delta y}{\Delta x}\\ \Delta x * 2e &= \Delta x * 2e + \Delta y\\ \end{aligned}$

也就是说我们定义一个$g$

$g = 2e * \Delta x$

那么就有了新的递增计算：

$g = g + 2* \Delta y$

新的初始值：

$\begin{aligned} e &= -0.5\\ 2e*\Delta x &= - \Delta x\\ g &= - \Delta x \end{aligned}$

到这里就完成了整数算法